| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- pca
- merge
- DataFrame
- dict
- p-value
- 교차검증
- pig
- 밀도기반
- k-means
- 분산분석
- T-검정
- cross validation
- hive
- SQL on 하둡
- 딕셔너리
- 다중공선성
- 유사도
- join
- 병렬 쿼리 시스템
- Sawzall
- 데이터프레임
- 하둡
- Python
- distribution
- SPLIT
- DBSCAN
- list
- 분포
- 결정계수
- 가설검정
- Today
- Total
one of a kind scene
평균의 종류(산술평균, 기하평균, 조화평균) 본문
평균의 종류(산술평균, 기하평균, 조화평균)
(궁금증이 생기게 된 계기)
- 모델의 성능을 평가하는 F1-score는 Precision과 Recall의 조화 평균을 사용하는 것을 보고 어떤 상황에 어떤 평균을 써야하는지에 대한 궁금증이 생김
1. 산술평균
• 일상 생활에서 가장 많이 사용하는 평균
• 각 요소의 총 합을 갯수로 나눈 것

2. 기하평균
• 각 요소를 곱한후 그 값에 루트를 씌운 값
• 일반적으로 성장률의 평균 등 상승률과 하락률을 활용한 계산에 유용하게 쓰임
• 예를 들어 1,000원의 주식이 10% 상승 후 10% 하락 했을 경우 산술적인 개념만 본다면 상승 +10% 하락 -10%로 ±10%이기 때문에 직관적으로 잘못 생각하여 가격 변동이 없다고 착각할 수 있음
• 하지만, 1,000원이 10% 상승하면 → 1,100원이 되고 1,100원이 10% 하락하면 → 990원이 됩니다
• 위 내용처럼 1,000원 짜리 주식이 990원이 되는 것을 상승률 10% 와 하락률 10%에 대한 기하 평균을 활용하여 계산해줄 수 있는데요.
• 수식으로 표현해보면 (1.1 x 0.9)^0.5 = 0.99 → 1,000원 x 0.99원 = 990 라는 결과를 얻을 수 있습니다

3. 조화평균
• 각 요소의 역수를 산술평균한 후 그 값을 다시 역수로 변환한 것
• 왕복속력을 계산할때, F1-Score 계산시 주로 사용
• 예를 들어 두 지점 A, B에 대하여 갈때는 시속 10Km/h, 올때는 시속 20Km/h로 왕복했다면,
평균속력은 조화평균인 13.33Km/h가 됩니다.
• (1/10 + 20/1)^(-1) = 2 x (3/20)^(-1) = 40/3 = 13.33

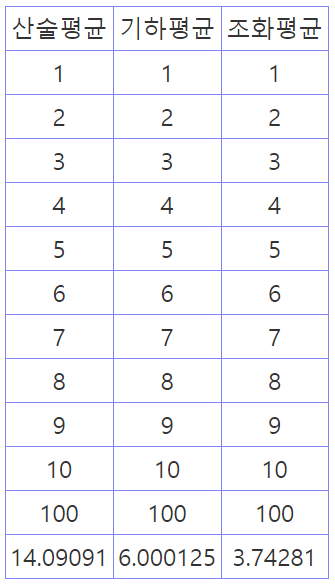
4. 산술평균 ≥ 기하평균 ≥ 조화평균

(심화1 : 산술평균 vs 기하평균 vs 조화평균)
• 각 평균의 종류의 상대적인 크기는 산술평균 > 기하평균 > 조화평균
• 1~10까지의 평균값은 5.5인데 단순 100이라는 이상치가 끼어들면서 산술평균이 가장 많이 상승함
• 이는 평균의 대표성을 띄고 있지 못하다고 판단할 수 있음
• 따라서, 상황에 따라서 적합한 대표성을 띄는 평균을 사용해야할 것이다
(심화2 : 조화평균 및 F1-score의 기하학적 의미)
• 조화평균의 기하학적 의미
• 아래 그림에서 서로 다른 길이의 A, B의 끝에서 다른 쪽의 base라인으로 선을 내렸을때, 만나는 점의 길이

• F1-score의 기하학적 의미
• 기하학적으로 봤을때 단순 평균이라기보다는 작은 길이 쪽으로 치우치게된, 그러면서 작은 길이 보다도 작은 평균이 도출됨
• 이렇게 조화평균을 이용하면 산술평균을 이용하는 것보다, 큰 비중이 끼치는 bias가 줄어든다고 볼 수 있음
• 즉, 아래 그림에서는 Precision보다 큰 길이(=비중)을 차지하는 Recall이 끼치는 bias가 줄어든 값으로 F1-score를 얻게됨

Reference
'데이터 분석 이론 > 일반' 카테고리의 다른 글
| 미분과 적분이란? 그리고 미분과 적분의 데이터 분석에서의 활용 (0) | 2020.04.17 |
|---|

